[中級編]LLMへ至る道~文章で類似度ってどういうこと？~[12日目]

LLMへ至る道 Advent Calendar 2023

#機械学習

#LLM

#自然言語処理

クルトン

2023.12.12

この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。

みなさんこんにちは！クルトンです。

前日のブログでは文脈を考慮して単語を埋め込んでみるモデルの、ELMoモデルについてご紹介しました。文脈を考慮して単語を埋め込んでみる為に、分散表現を得るための工夫が今までのモデルを使って改良されていたものでしたね。

本日は分散表現を得たものに対して、「似ているかどうか」という判定をするための指標についてご紹介していきます。

文章が似ているってどういうものを想像しますか？

みなさんは文章が似ているってどういうものを想像しますか？自分は以下のようなものを想像しました。

猫が私の椅子で寝ている
猫が私のベッドで寝ている

上記の例は自分がよく日常で目にしている内容で、我が家の猫に場所をお譲りする事が多いから頭に出てきた情景でございます。

文章という観点でいうと主語が「猫」で動詞が「寝ている」ですので、場所は違うものの、似ている文章といえるのではないでしょうか？

ただし、コンピュータに対して上記のような説明をしても伝わりません。それはコンピュータが数値を介して現象を理解する性質を持っているからです。

ここで思い出して欲しいのは、我々が使っている自然言語をコンピュータが取り扱えるようにしたものを分散表現と呼ぶ事です。

コンピュータが文章を理解するためには分散表現、つまり「ベクトルを使っている」というところがポイントです。

ベクトル同士が似ているか確認するものがある

ここで、ベクトル同士を比べるコサイン類似度というものがあります。

コサイン類似度について数式を見ていきましょう。xというベクトルとyというベクトルがある場合は、以下のように定義されます。

$cosine similarity = \frac{⟨x,y⟩}{||x|| ||y||}$

パッと見て分からない方は、⟨x,y⟩がxとyのベクトル(向きと大きさ)で、||x|| ||y||がそれぞれのベクトルの大きさだと捉えてください。

つまり日本語にして書くと以下のようになります。

$コサイン類似度 = \frac{2つのベクトルの大きさと向き}{2つのベクトルの大きさ}$

右辺の計算の結果、何が出てくるでしょうか？

答えは簡単で、向きです。

コサイン類似度と言っていますが、向きをチェックしているものです。

ここまで文章だけで確認してきた内容を、イメージにしたものが下図になります。

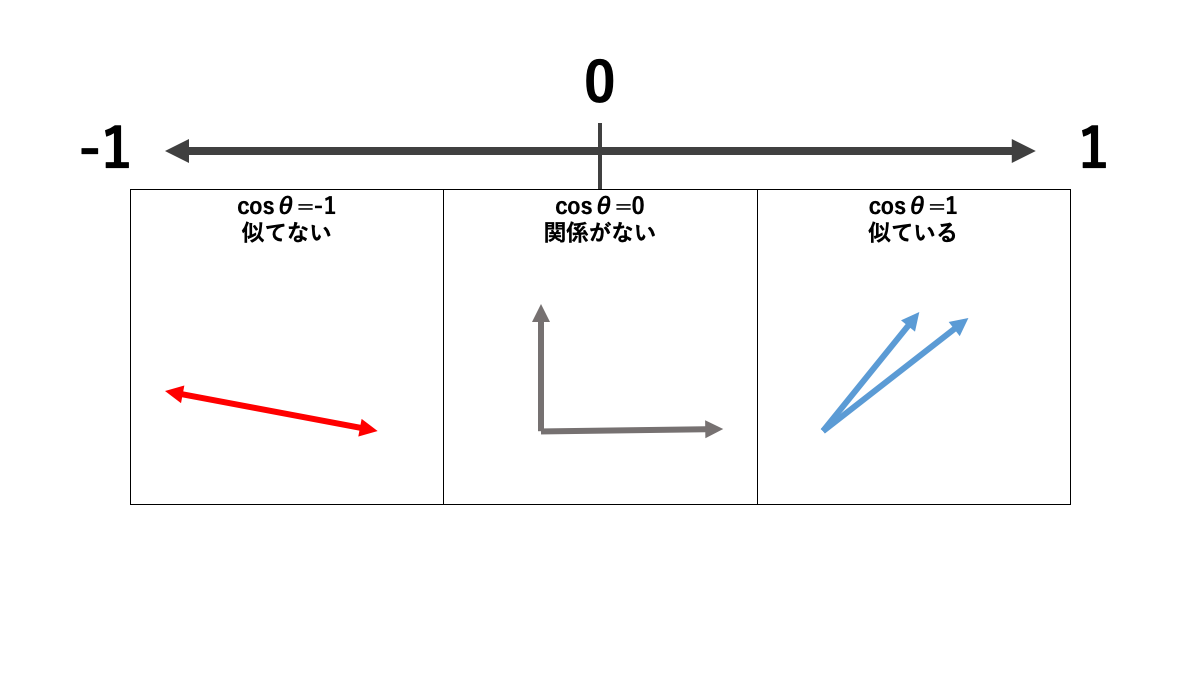
road-to-llm-advent-calendar-2023-12-01

-1から1の範囲で値が収まっていますが、これは大きさ同士を割り算しているためです。例えば-8を8で割れば-1になりますし、8を8で割れば1になりますよね。先程の式で、大きさのみを表していた数式||x|| ||y||は、大きさを求めるためにマイナスの符号を取った数値を取得しています。

コサイン類似度を求めてみた

具体的に簡単なコードで内容をチェックする方法を紹介します。

Google Colab(ランタイムはCPU)で実行していきます。

似ている

似ている場合の計算です。

import numpy as np
x_vector = np.array([0.1, 0.13])
y_vector = np.array([0.02, 0.2])
np.dot(x_vector,y_vector)/(np.linalg.norm(x_vector)*np.linalg.norm(y_vector)) # コサイン類似度の定義式通りに計算

出力結果は0.8493588352433417となりました。かなり似ているようです。

無関係

無関係の場合です。

import numpy as np
x_vector = np.array([0.000000000000001, -0.0000000000000001])
y_vector = np.array([0.02, 0.2])
np.dot(x_vector,y_vector)/(np.linalg.norm(x_vector)*np.linalg.norm(y_vector)) # コサイン類似度の定義式通りに計算

あまりにも片方のベクトルの値が小さいため、出力は0.0となり無関係であると判断されました。

似ていない

似ていない場合です。

import numpy as np
x_vector = np.array([-0.1, -0.1])
y_vector = np.array([0.02, 0.2])
np.dot(x_vector,y_vector)/(np.linalg.norm(x_vector)*np.linalg.norm(y_vector)) # コサイン類似度の定義式通りに計算

出力結果は-0.773957299203321となりました。マイナスの値しか入っていないベクトルと、プラスの値しか入っていないベクトルなので、確かに似てないような気がしますね。